Моделирование процессов терморегуляции в гнездах зимующих пчел

УДК 574.24/51-76

Медоносная пчела заняла широкий ареал за счет освоения зон с умеренным и холодным климатом, что сопряжено с развитием адаптаций к длительной зимовке. Ее преодоление достигается созданием больших запасов корма и их экономного расходования благодаря минимизации локомоций и затрат энергии на терморегуляцию. Оптимальный ответ пчелиной семьи на охлаждение — результат усилий всех взрослых пчел, реагирующих на изменения внешней температуры агрегированием в межсотовых пространствах, генерацией тепла и регулированием газовых потоков, связанных с потреблением кислорода и выделением диоксида углерода.

В гнездовом скоплении зимующих пчел, по крайней мере в ее тепловом центре, поддерживается температура, обеспечивающая возможность внутригнездовых миграций. К ним насекомого побуждает необходимость пополнения его индивидуальных кормовых запасов и локализации в зонах, соответствующих его физиологическим потребностям. Центральная зона гнезда — зона пополнения индивидуальных запасов корма и зона высокой концентрации углекислого газа, действие которого на хеморецепторы усиливается температурой. В тепловом центре — 28...37°С [1, 2].

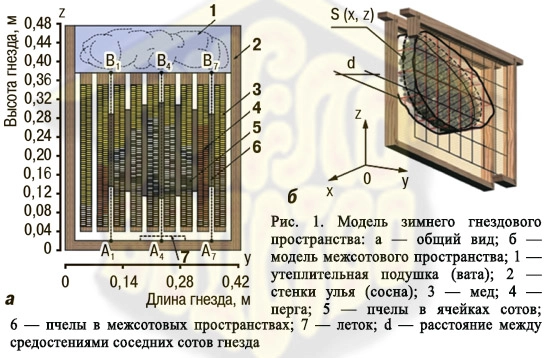
Исходя из сказанного, оптимизация зимовки пчелиных семей достигается регуляцией  внешней температуры и воздухообмена внутригнездового пространства с окружающей средой. Для изучения этих процессов мы попытались создать математическую модель теплопродукции, теплоотдачи и теплонакопления в межсотовых скоплениях пчел (клубе) зимующих семей (Модель зимнего гнездового пространства: 9 рамок 435х300 мм; 7 рамок занятые пчелами, 2 медовые без пчел; х, у, z — размеры модели: ширина, длина, высота). В процессе моделирования исходили из предположения, что межсотовые скопления пчел представляют собой пористые структуры, в которых дыхательно-газовые смеси обусловливают процессы конвективного теплообмена, а вертикальная асимметрия распределения температурных полей связана с удалением продуктов метаболизма и поступлением свежего воздуха. Что же касается динамики этих процессов, то они в каждом конкретном случае зависят от геометрии скопления, направления потоков теплоты и от теплоносителя.

При моделировании переноса тепла исходили из того, что пчелы, агрегируясь в межсотовых пространствах, образуют единую систему с тепловой конвекцией. Часть пространства между двумя сотами, занятая пчелами, моделируется цилиндром (рис. 1) с перпендикулярной к плоскости сотов координатной осью y и основаниями, параллельными плоскости смежных сотов, площади которых равны S (x, z). Поэтому все скопление (клуб) в зависимости от численности пчел в нем и внешней температуры разбивается на 6–7 фигур, близких по форме к цилиндрам и разделенных участками сотов с ячейками, занятыми медом, пергой и воздухом. Исходя из этого, к основным механизмам теплопередачи внутри «цилиндров» отнесены перенос тепла через пчел (теплопроводность) и конвективная теплопередача, обусловленная движением метаболитов и миграцией отдельных насекомых. На внешней боковой границе «цилиндров» рассматривается ньютоновская теплоотдача, исключается теплоотдача испарением, а на участках скопления пчел, граничащих с сотами, теплообмен происходит только за счет теплопроводности.

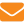
В указанных предположениях уравнения теплопроводности, фильтрации и неразрывности имеют вид (сохранены обозначения, принятые в системе компьютерной математики Comsol 3.5):

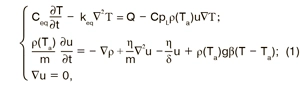
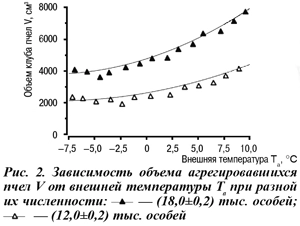
где u — вектор скорости дыхательно-газовой смеси, м/с; T — температура, °К;T_a — температура внешней среды, °К; ρ(Т_а) — плотность дыхательно-газовой смеси (теплоносителя), кг/м³; p — давление, Па; m — пористость (Пористость — безразмерная величина, характеризующая количество пор в скоплении пчел, в расчетах вычисляется как отношение объема пор к объему скопления); δ — проницаемость, м²; η — динамическая вязкость, Па·с; β — коэффициент теплового расширения, 1/°K;Сp_L — теплоемкость дыхательно-газовой смеси при постоянном давлении, Дж/(°К·кг); g — вектор ускорения свободного падения, м/с²; С_eq— эквивалентная теплоемкость теплоносителя и пористой среды (кг/м³)·Дж/(°К·кг); k_eq— эквивалентная теплопроводность теплоносителя и пористой среды Вт/(°К·м); Q — теплопродукция пчел, Вт.

Эквивалентные значения теплоемкости и теплопроводности дыхательно-газовой смеси и пористой среды определяются соответственно из следующих соотношений:

где θ_L — относительный объем дыхательно-газовой смеси в скоплении пчел; θ_p — относительный объем пчел в скоплении; Cp_p — теплоемкость пористой среды при постоянном давлении; p_p — плотность пористой среды; k_L и k_p — соответственно теплопроводности дыхательно-газовой смеси и пористой среды.

Каждое из рассматриваемых дифференциальных уравнений системы (1) выражает определенный закон сохранения: первое — закон сохранения энергии и содержит четыре члена: нестационарный, кондуктивный, источниковый и конвективный; второе определяет поле скорости, которое должно удовлетворять дополнительному ограничению, а именно закону сохранения массы или уравнению неразрывности (третье уравнение). Выражение ρ(T_a)gβ(T–T_a) моделирует естественную конвекцию, связанную с изменением градиента температур в различных зонах скопления.

Граничные условия для первого уравнения системы (1) выбираются по Ньютону с коэффициентом теплоотдачи h, во втором уравнении давление вне скопления пчел выбрано равным атмосферному.

Определение теплофизических параметров системы уравнений (1) осложняется их зависимостью от состояния пчел, принимающих в одно и то же время разное участие в терморегуляции [3]. Например, многочисленные попытки представления проницаемости через пористость и характерные размеры для типичных пористых сред как путем рассмотрения простейших моделей, так и путем обработки экспериментальных данных носят частный характер и имеют узкую область применения. Поэтому целесообразно ограничиться теми интервалами, в пределах которых могут изменяться анализируемые теплофизические параметры. При расчетах использовали геометрические параметры скопления пчел, полученные из анализа термограмм [3, 4]. Так, например, изменение объема скопления было смоделировано по тепловизионным термограммам для семей численностью (12±0,2) и (18±0,2) тыс. пчел (рис. 2).

Определение пределов изменения объема скопления в зависимости от внешней температуры позволяет прослеживать динамику плотности пчел в скоплении, а значит, и пористость m, границы которой задаются интервалом 0,3≤m≤0,8. Тогда, используя формулу Козени-Кармана [6], можно оценить границы изменения проницаемости δ:

где d — средний размер пор. Пределы изменения остальных физических величин выбраны в соответствии с работой [2].

Сформулированную задачу решали аналитическими методами и методом конечных разностей в пакете COMSOL 3.5. Численные решения анализировали с использованием двух готовых модулей (прикладных режимов): модуля фильтрации «Earth Science Module → Fluid Flow → Brinkman Equations» и модуля теплообмена «Heat Transfer Module → General Heat Transfer». Система COMSOL сама внутренними средствами строит из этих прикладных режимов систему связанных уравнений и находит совместное решение фильтрационной и тепловой задач.

Приведем некоторые результаты модели (рис. 3) холодовой агрегации пчел при оптимальных (теплопродукция и теплоотдача сохраняются на постоянном уровне) значениях внешней температуры. Область оптимума соответствует минимальному физиологическому контролю и минимуму энергетических затрат для поддержания пчелами гомеостаза и охватывает широкий интервал температур: –3,0…+8,8°С [5].

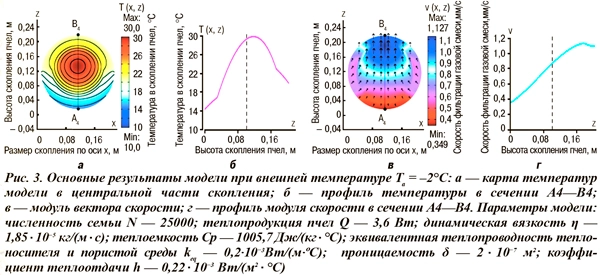
Учет конвективного теплопереноса приводит к вертикальной асимметрии распределения температурных полей (см. рис. 3 а, б), что не наблюдается в математических моделях, учитывающих только теплоперенос теплопроводностью пчел [2, 7, 8]. При этом в указанном выше интервале внешних температур тепловой центр смещается к нижней поверхности скопления с уменьшением внешней температуры.

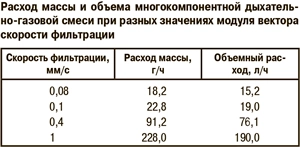Этот результат согласуется с тепловизионными исследованиями тепловых процессов в скоплениях пчел, стимулируемых охлаждением, но не находит объяснения в предыдущих теоретических моделях [7, 8]. В зоне температурной оптимальности расчетные значения модуля вектора скорости фильтрации находятся в интервале 0,1–1,5 мм/с. При этом интенсивность конвективного движения выше на верхней поверхности скопления пчел (см. рис. 3 в, г), где поддерживается более стабильная температура в пределах 20...24°С. При приближении внешней температуры к нижней границе зоны оптимальности модуль вектора скорости уменьшается, поэтому теплопроводность начинает доминировать над конвективным механизмом теплопереноса. Интересно сравнить расчетные значения количества потребления воздуха пчелиной семьей численностью 25 тыс. пчел при разных скоростях фильтрации (табл.), полученные из результатов моделирования. Есть основания полагать, что примерно 25–30% выдыхаемой многокомпонентной смеси составляет водяной пар, а дыхательный коэффициент при окислении углеводов близок к единице. Эти обстоятельства позволяют рассчитать количество потребляемого пчелами меда. Так, при средней скорости фильтрации 0,1 мм/c количество расчетного потребления меда пчелиной семьей численностью 25 тыс. пчел при температуре –2°С составляет 1,2 г/ч или 28,8 г/сут, что соответствует среднестатистическим данным потребления корма в зимний период [1]. При этом в скопление поступает воздух в количестве 19,0 л/ч, и надо полагать только часть этого воздуха проходит через дыхательную систему пчел, остальная часть, смешиваясь с выдыхаемыми пчелами газами, составляет конвекционный ток.

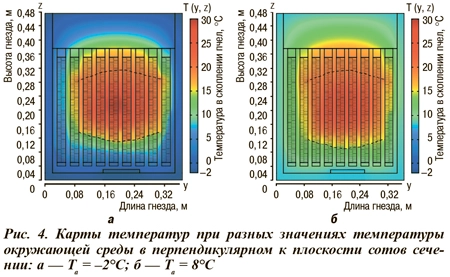Более сложная задача моделирования всего внутриульевого пространства с учетом всех сотов с медом, пергой и находящимися на них пчелами при наличии свободной конвекции в гнезде была решена комбинированием аналитических и численных методов (рис. 4). Совершенно очевидно, что пчелы регулируют тепловой режим только внутри скопления, а расчет остальной части гнезда представляет интерес с точки зрения обеспечения оптимальных условий зимовки пчел. При этом возникающая в улье конвекция обусловлена вырабатываемым пчелами теплом, а удаление дыхательно-газовой смеси и поступление свежего воздуха представляют собой сложный цикл воздухообмена и вентиляции, зависящий не только от внешней температуры, физиологического состояния пчел, геометрических параметров гнезда и самого скопления, но и от большого числа других факторов. В рассмотренной модели был сделан ряд упрощений без ущерба существенным свойствам механизмов терморегуляции в скоплении зимующих пчел.

Численное решение модели (1) позволяет оценить значения всех основных переменных (температура, скорость фильтрации, давление) практически для всего внутриульевого пространства при оптимальных значениях внешней температуры. При этом можно моделировать многие идеализированные условия, например: постоянство температуры в тепловом центре, динамику изменения этой температуры при фиксированных значениях отдельных параметров модели, роль конвективного члена в уравнении (1) и т.д. Очевидно, ни в одном экспериментальном исследовании невозможно измерить распределения всех переменных во всей исследуемой области. Поэтому результаты численного моделирования могут служить дополнением и подтверждением имеющейся экспериментальной информации. Естественно, полезность этих расчетов ограничена обоснованностью математической модели (1).

На данной модели количественно исследован вклад отдельных составляющих (конвекция, теплопроводность через пчел) в общий теплообмен при оптимальных (когда теплопродукция и теплоотдача сохраняются на относительно постоянном уровне) значениях внешней температуры. Для полного понимания терморегуляции пчел фундаментальное значение имеют количественные знания о процессах теплопереноса внутри скопления пчел, особенно на поверхностном слое, при оптимальных и неоптимальных значениях внешней температуры. При этом, как показывают проведенные в данном исследовании расчеты, познавательную и практическую ценность получаемых результатов в значительной степени определяют правильно сформулированная содержательная модель и математическая постановка расчетной задачи, основанные на анализе имеющихся экспериментальных данных.

Основное ограничение представленной модели обусловлено рассмотрением механизмов терморегуляции при оптимальных значениях внешней температуры. Для моделирования процессов теплопереноса при температуре ниже –5°C потребуется куда более сложная геометрия. Ограниченность и неточность сведений о структуре скопления как пористой среды с сочетанием разных масштабов фильтрационных процессов не позволяет в этом случае построить однозначную модель. Кроме того, наличие у пчел волосков длиной 0,7–1,1 мм, с одной стороны, увеличивает эффект изоляции, а с другой — уменьшает скорость удаления метаболитов. Вопрос о тепловой эффективности волосков в скоплениях пчел остается открытым и, вероятно, не может быть изучен прямыми измерениями. Отметим также, что пчелы при низких температурах используют принудительную конвекцию, при которой изучение движения дыхательно-газовой смеси и перемещения пчел в скоплении прямым применением обычных методов гидродинамики, то есть решением уравнений движения вязкой жидкости для области, представляющей собой совокупность всех пор, становится затруднительной.

Исследование выполнено в рамках базовой части государственного задания Министерства образовании и науки России.

Е.К.ЕСЬКОВ, В.А.ТОБОЕВ

Проведен численный анализ естественной конвекции в скоплении пчел при наличии внутреннего тепловыделения. Показано, что пчелы используют разные механизмы теплообмена в зоне оптимальных для зимовки значений внешней температуры. При неоптимальных значениях внешней температуры конвективный теплообмен становится вынужденным, что связано с уплотнением пчел и дополнительным выделением тепла для поддержания гомеостаза.

Ключевые слова: скопления пчел, температура, теплоперенос, моделирование, скорость фильтрации, проницаемость.

ЛИТЕРАТУРА
1. Еськов Е.К. Экология медоносной пчелы. — Рязань: Русское слово, 1995.
2. Еськов Е.К., Тобоев В.А. Математическое моделирование распределения температурных полей в холодовых агрегациях насекомых // Биофизика. — 2009. — Т. 54. — Вып. 1.
3. Еськов Е.К., Тобоев В.А. Сезонная динамика тепловых процессов в межсотовых скоплениях зимующих пчел Apis mellifera // Зоол. журнал. — 2011. — Т. 90. — №3.
4. Тобоев В.А. Современные методы изучения теплового гомеостаза // Пчеловодство. — 2006. — №10.
5. Тобоев В.А. Теплофизическая модель холодовой агрегации пчел // Пчеловодство. — 2007. — №1.
6. Ocko S.A., Mahadevan L. Collective thermoregulation in bee clusters // J. Royal Society Interface. — 2014. — V. 11. — №91.
7. Omholt S. Thermoregulation in the winter clusters of honeybee Apis mellifera // J. Theor. Biol. — 1987. — V. 128.
8. Sumpter D., Broomhead D. Shape end dynamics of thermoregulating honey bee clusters // J. Theor. Biol. — 2000. — V. 204.

СВЕДЕНИЯ ОБ АВТОРАХ:
Еськов Евгений Константинович, д-р биол. наук, проф., заслуженный деятель науки и техники, декан факультета охотоведения и биоэкологии РГАЗУ;
Тобоев Вячеслав Андреевич, д-р биол. наук, проф. Чувашского ГУ.

MODELING OF PROCESSES OF THERMOREGULATION IN THE BROOD NESTS OF WINTERING BEES

E.K.Eskov, V.A.Toboyev

The article deals with mathematical model of cnvective heat transfer in honey bee cluster, with saturated respiratory mixture and internal heat. It is analyzed the influence of temperature parameters, heterogeneity factors density and number of honey bee clusters, on heat transfer modes. It is shown that honey bees use different heat exchange mechanism in optimal range of external temperature in winter. In non-optimal range of external temperature, convective heat transfer becomes forced, due with additional honey bee heat to maintain homeostasis.

Keywords: honey bee clusters, temperature, heat transfer, modeling, seepage velocity, permeability.

«

• 1
• 2
• 3
• 4
• 5

»