![]() Проведенные исследования показывают, что акустический шум пчелиной семьи может дать пчеловоду определенную информацию об ее состоянии (Е.К.Еськов, 1979). Какие методы анализа этого показателя используются? В основном спектральный. Однако шум пчелиной семьи нельзя считать стационарным, поэтому эти методы недостаточно эффективны. О применении спектрального анализа мы уже писали в журнале «Пчеловодство» №4, 2003 (В.Э.Дрейзин, А.Ф.Рыбочкин, И.С.Захаров).
Проведенные исследования показывают, что акустический шум пчелиной семьи может дать пчеловоду определенную информацию об ее состоянии (Е.К.Еськов, 1979). Какие методы анализа этого показателя используются? В основном спектральный. Однако шум пчелиной семьи нельзя считать стационарным, поэтому эти методы недостаточно эффективны. О применении спектрального анализа мы уже писали в журнале «Пчеловодство» №4, 2003 (В.Э.Дрейзин, А.Ф.Рыбочкин, И.С.Захаров).
Сейчас нет эффективных и достаточно дешевых приборов, позволяющих анализировать звуки семей, что могло бы существенно облегчить работу с пчелами. Если и появляются разработки, то они скорее предназначены для работы в качестве детектора их состояния.
Как уже сообщалось, состояния семей характеризуются кодовыми сообщениями. Формирование кодов основано на попарном сравнении интенсивных составляющих частотного спектра. Разрядность двоичного кода зависит от числа исследуемых интенсивных составляющих. Так, если исследуется четыре интенсивные составляющие, то разрядность кода, полученная при попарном сравнении, r=6. Кодовые сообщения семей характеризуются разной частотой появления, что хорошо заметно только при длительном прослушивании.
 По одной короткой выборке длительностью в одну секунду нельзя сделать вывод о процессах, происходящих в семье, поскольку они подвержены постоянному изменению. Для их анализа возможны различные варианты. Необходимо построение динамической картины «акустического портрета», анализ по среднему коду (ж-л «Пчеловодство» №4, 2003). Так как коды появляются с различной частотой, то для их исследования применимы методы вероятностного анализа. Выполняется это так. Первоначально образуются двоичные коды в виде сообщения, приведенного на рис. 1.
По одной короткой выборке длительностью в одну секунду нельзя сделать вывод о процессах, происходящих в семье, поскольку они подвержены постоянному изменению. Для их анализа возможны различные варианты. Необходимо построение динамической картины «акустического портрета», анализ по среднему коду (ж-л «Пчеловодство» №4, 2003). Так как коды появляются с различной частотой, то для их исследования применимы методы вероятностного анализа. Выполняется это так. Первоначально образуются двоичные коды в виде сообщения, приведенного на рис. 1.
Здесь представлено ограниченное число двоичных кодов, которое определяется длительностью прослушивания шума пчелиной семьи, но оно может достигать ста и более.
Экспериментально установлено, что длительность прослушивания (то есть первая выборка) должна быть от 2 до 10 мин (фиксация состояния роения может потребовать меньше времени). Следует подчеркнуть, что оснащение пасек соответствующими техническими системами позволит установить оптимальное время диагностирования, при котором можно с полной уверенностью сделать вывод о процессах в семье.
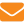
 На рис. 2 приведены графики изменения среднего значения единиц двоичных кодов (В) и среднего значения чисел (А, С), полученных при перекодировании двоичных кодов в десятеричные и восьмеричные.
На рис. 2 приведены графики изменения среднего значения единиц двоичных кодов (В) и среднего значения чисел (А, С), полученных при перекодировании двоичных кодов в десятеричные и восьмеричные.
Как было сказано ранее, коды, характеризующие состояния пчелиных семей, появляются с различной частотой, что позволяет говорить о вероятности их появления, а следовательно, об энтропии. Неопределенность, то есть энтропию контролируемого состояния пчелиной семьи определяют по формуле
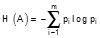 , где
, где 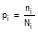 , ni — частота наблюдаемого кода; Ni — число кодов i-го состояния семьи.
, ni — частота наблюдаемого кода; Ni — число кодов i-го состояния семьи.
На рис. 2 хорошо видно, что неопределенность уменьшается [Н(В)а0] при приближении времени выхода роя, что характерно для 6 и 8 состояний. Энтропия Н(В) увеличивается при организации отводков (14 и 16).
Семья, которая находится в рабочем состоянии и к нужному сроку достигает максимальной продуктивности, при количестве кодов N=31 код 0 встречается 78 раз, код 1–13 раз, код 2–5 раз, код 3–8 раз, код 4–6 раз, код 5–2 раза, код 6–11 раз, код 7– 63 раза. Здесь параллельный двоичный код (пример двоичного кода приведен на рис. 1) перекодирован в последовательный восьмеричный. Определив энтропию данного состояния пчелиной семьи для двух вариантов кодирования, мы установили Н<2>=1,19 бит, Н<8>=2,12 бит, то есть результаты практически равные.
Следовательно, при построении распознающих устройств для анализа акустического сигнала пчелиной семьи необходимо учитывать не только средний код, но и энтропию Н(В), которая может явиться дополнительным информативным показателем.
А.Ф.РЫБОЧКИН
г. Курск, КГТУ

Cодержание пчел в двухстенных ульях…
авг 19, 2018
Расширение пасеки
фев 13, 2021
Новое в лечении аспергиллеза пчел…
июль 4, 2019
Аскозол - новый препарат для лечения аск…
окт 1, 2014
Печатный расплод — товарная продукция…
окт 29, 2016
Лечебно-профилактические работы на пасек…
апр 3, 2019
Гемолимфообращение в крыльях пчел…
июнь 17, 2014
Любите пчел
нояб 1, 2023
О некоторых нормативно-правовых актах, р…
янв 11, 2017
Медопродуктивность синюхи голубой…
июнь 20, 2024
Подушка-кормушка и утепленный улей…
июнь 27, 2021
Несколько слов о моем учителе профессоре…
фев 18, 2017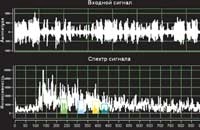
Анализ акустического шума пчелиной семьи…
нояб 20, 2016
Адаптивная технология содержания пчел…
мая 31, 2016
Заболевания пчел в жаркое лето…
июнь 8, 2014











 Адрес редакции журнала "Пчеловодство":
Адрес редакции журнала "Пчеловодство":