Процессы Маркова, в частности гибели и размножения, используют для описания работы и анализа широкого класса систем с конечным числом состояний, в которых происходят неоднократные переходы из одного состояния в другое под воздействием каких-либо причин. В таких системах они происходят случайным образом, скачкообразно в произвольный момент времени, когда наступают некоторые события (потоки событий). Как правило, они бывают двух типов: одно из них условно называют рождением объекта, а второе — его гибелью.
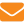
Естественное размножение пчелиных семей — роение — с точки зрения протекающих в системе в текущий момент времени процессов можно рассматривать как вероятностный процесс, когда семья в определенный момент времени может перейти из рабочего состояния в роевое. В зависимости от различных факторов, как контролируемых технологических, так и слабоконтролируемых биологических и климатических, оно может закончиться роением или возвратом семьи в рабочее состояние. При этом семья может неоднократно переходить то в одно, то в другое состояние. Таким образом, для описания математической модели процесса роения допустимо применять теорию однородных процессов Маркова.
В марковских процессах гибели и размножения для системы с конечным числом состояний (n+1) предельные вероятности обоих событий определяют с использованием специальных формул (Вентцель, 1991).
Интенсивность перехода пчелиной семьи в роевое состояние λ — размножение — в значительной мере определяется темпами накопления молодых бездеятельных пчел. Интенсивность обратного перехода μ — «гибели» — возвращением семьи в рабочее состояние, которая, в свою очередь, зависит собственно от роения, отбора расплода и пчел (формирование отводков), количества собираемого нектара и т.д.
Вероятность перехода пчелиной семьи в роевое состояние в первую очередь будет определяться интенсивностью проходящих в ней процессов, приводящих к роению λ, и противороевых приемов μ, которые зависят от технологий, используемых для снижения ройливости семей. Следовательно, чтобы влиять на обсуждаемые процессы, необходимо изменить интенсивность и направленность потоков λ и μ (рис. 1).
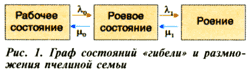Моделирование отбора части расплода из семьи, то есть уменьшение интенсивности появления молодых особей в ней для предотвращения роения (рис. 2), показало, что вероятность сохранения рабочего состояния возрастает пропорционально количеству расплода, изъятому из гнезда (вероятность роения соответственно пропорционально уменьшается). Однако отбор четырех-пяти рамок способствует этому процессу только до величины 0,5-0,7 (для разных по развитию семей), то есть вероятность роения и роевого состояния остается на достаточно высоком уровне.
Моделирование замены плодной пчелиной матки на неплодную приведет к тому, что минимум через 21 день после этой операции, независимо от даты ее смены, вероятность роения будет равна нулю. Если старую матку заменяют молодой плодной, то вероятность возвращения в рабочее состояние несколько возрастает, а роения уменьшается, однако вероятность последнего события в среднем 0,2-0,4.
Моделирование отбора из семьи части пчел (увеличения их «гибели») показало, что вероятность возникновения рабочего состояния логарифмически возрастает, а вероятность роения логарифмически сокращается. При противороевом приеме — отборе из семьи 5–7 тыс. пчел (две-три стандартные рамки) — вероятность роения составит 0,05, а вероятность рабочего состояния — 0,8; отбор более трех рамок с пчелами снижает вероятность роения на очень малую величину.
Рассмотрим случай изменения вероятности рабочего состояния и роения при отборе из гнезда расплода и пчел. Результаты моделирования для средней семьи представлены в таблице.
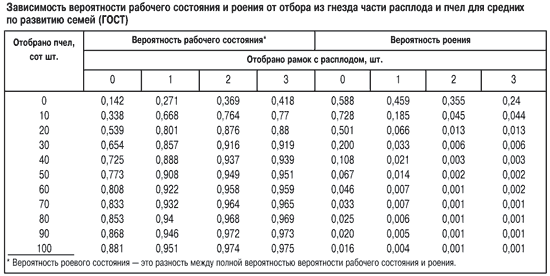
При одновременном отборе расплода и пчел вероятность роения резко уменьшается, а рабочего состояния увеличивается. Так, для уменьшения вероятности роения до Р=0,002 у пчелиной семьи, имеющей на дату моделирования 35 тыс. пчел (3,5 кг), достаточно отобрать около трех рамок с расплодом старших возрастов (10–12 тыс. ячеек) и столько же пчел (5–6 тыс. пчел), то есть сократить семью на 15–17%. Аналогичный результат получается при уменьшении слабых пчелиных семей на 20–25%, а сильных семей на 10–11%. Моделирование показывает, что отбор большего количества расплода и пчел, в том числе использование приема деления на пол-лета, практически не влияет на снижение вероятности роения и незначительно увеличивает (в среднем на 1,0–2,5%) вероятность рабочего состояния.
Следовательно, для оценки состояния роения необходимо определить интенсивность вероятностных процессов, приводящих семью в рабочее или роевое состояние. Причем это зависит как от экзогенных, так и от эндогенных факторов, в том числе от сокращения интенсивности накопления избытка молодых бездеятельных пчел.
Результаты моделирования роения и некоторых противороевых приемов перехода пчелиной семьи из рабочего состояния в роевое и обратно с использованием марковских процессов в целом подтверждаются практикой.
Следует отметить, что в отличие от всех известных биологических объектов для пчелиной семьи переход из состояния размножения (роевого) к исходному рабочему не сопровождается гибелью семьи, что подчеркивает уникальные свойства медоносных пчел.
И.Н.МИШИН
Смоленский
сельскохозяйственный институт
Адрес редакции журнала "Пчеловодство":
