Почему пчелы строят шестигранные ячейки? Такой вопрос наверняка задает каждый, кто видит удивительное инженерное сооружение — соты, заполненные медом. Ответ можно найти, если обратиться к истории развития пчел...
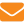
Давным-давно пчелы жили каждая сама по себе и строили отдельные домики-гнезда в виде трубочек со сферическим дном (рис. 1). Такие насекомые есть и сейчас, например в Индии. Они строят свои жилища в дуплах деревьев, в расщелинах скал и в пещерах, а иногда просто на ветках.
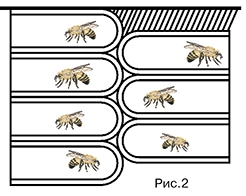
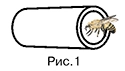Чтобы вместе защищаться от врагов, пчелы стали строить свои домики, прикрепляя их друг к другу, а верхний ряд — к жесткому основанию (рис. 2). Так как удобных для гнездования мест сравнительно мало, а пчел много, то вследствие тесноты при одновременной отстройке вместо отдельных цилиндриков естественным образом получались многогранники, а вместо полусферических донец — пирамидки (рис. 3). Каждая ячейка соприкасалась с шестью другими такими же шестигранниками.
А что же пчелы? Они из индивидуальных особей стали коллективными насекомыми, что позволило пчелам сохраниться как виду при резком изменении климата. Этому способствовали почти двукратное сокращение расходов воска на отстройку ячеек и сроков изготовления сота; высвобождение массы пчел для сбора нектара и создания зимних кормовых запасов. Поскольку стенки ячеек стали тоньше, каждая особь начала обмениваться теплом с девятью соседними: с шестью — через стенки, с тремя — через грани донца.
Изобретение рамочного улья, медогонки и вощины резко повысило производительность труда пасечника и медопродуктивность пчелиных семей. Однако в пчеловодстве еще много неразгаданных тайн и загадок. Например, оказалось, что пчелы — замечательные математики. При минимальном расходе материала они отстраивают оптимальные по вместимости и прочности конструкции. Не случайно в ракетно-космической технике используются сотовые панели, а в строительстве — ячеистый бетон.
Экскурс в прошлое пчел позволяет полнее понять геометрию ячеек и установить их основные параметры. Рассмотрим четыре соприкасающихся полусферических донца (рис. 4).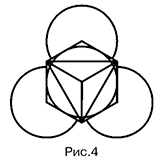
Если через точки соприкосновения провести плоскости, касательные к сферам, до их пересечения между собой и с гранями шестигранника, то получим пирамиду, сложенную из трех ромбов, большие диагонали которых на рисунке отмечены пунктиром. Их длину можно принять за характерный размер ячейки, поскольку она совпадает с диаметром d вписанной в шестигранник окружности. В дальнейшем треугольник, составленный из диагоналей ромбов, будем принимать за основание пирамиды донца ячейки.
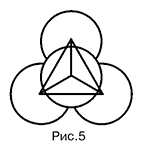Для облегчения определения характерных размеров ячейки выполним дополнительное построение: соединим центры четырех сфер (рис. 5). Получился тетраэдр, причем точки соприкосновения сфер находятся посередине его ребер. Длина ребра тетраэдра будет диаметром d ячейки. Через него можно выразить все остальные величины.
Параметры тетраэдра легко вычислить. Так, углы наклона ребер к основанию составляют 54,7356°, граней — 70,5288°.
Отметим, что боковые ребра тетраэдра ортогональны к соответствующим граням основания ячейки. В свою очередь, боковые ребра основания ячейки ортогональны к граням тетраэдра. Вычитая приведенные выше величины из 90°, получим углы наклона граней основания ячейки и ребер — стыков двух таких граней. Они соответственно будут равны 35,2644° и 19,4712°. Далее можно определить острый (70,5288°) и тупой (109,4712°) углы ромбов, а также двугранный угол между их плоскостями — 120°.
Углы ромбов обычно приводятся в популярных изданиях для пчеловодов. Однако для конструкторов важны и другие параметры ячеек. Возможно, эти результаты и наглядный способ их получения будут полезны при разработке нового оборудования для получения вощины.
А.Н.ВЕРЕЩАГИН
г. Пермь
Адрес редакции журнала "Пчеловодство":
